Intro to Binary Numbers & Bitwise Operations - Ultimate Visual Guide
Learn everything you need to know about bit operations in this interactive and visual guide.A brief intro to binary numbers
In the following article we will start with the basics of binary numbers and common operations. We will build-up from there to more complex masking and iterative functions and even look at underlying representation methods such as IEEE floating-point representation and complement number representation.
A few examples where you might find binary numbers commonly used today:
- Compressed Data - For example when transferring data between socket connections you'll most likely be dealing with binary data
- Encryption/Compression Algorithms - Encryption and compression algorithms are often built using binary operations (e.g., Huffman coding)
- Bit flags - For example assigning security levels of a user (e.g., User=0001, Admin=0010)
- Bit masks - Very common in image processing and games systems (e.g., alpha masks, collision layers, etc.)
Learning Python?
I mostly use Python throughout this blog as I find it to be a clean and intuitive language that is well-suited to teaching core programming concepts.
If you're unfamiliar with Python (or just want to brush up), checkout Best Python Courses According to Data Analysis for course recommendations.
Base-2 vs. base-10 number systems
Binary numbers use the base-2 numeral system rather than our everyday base-10 system. In base-2 we represent numbers with just 2 digits, 1s and 0s, so the number 2 as a 4-bit binary number is represented as 0010.
Let's look at two examples, the first is in our standard base-10 (decimal) system and the second is in our base-2 (binary) system:
Base-10 (decimal) number system
Raise each place by powers of 10: 1,2,5 = 100+20+5 = 125
Base-2 (binary) number system
We raise each place by powers of 2: 1,1,0,1 = 8+4+0+1 = 13
Bitwise Operators
Aside from standard mathematical operators such as +, -, *, programming languages also have bitwise operators for bit-shifting and various comparisons.
We'll briefly explore all the standard operations in these next few sub-sections:
AND operations
Bitwise AND : &
The & operator when applied to two sets of bits returns 1 only if both corresponding bits are 1.
You can think about this similar to a multiplier symbol on each bit (e.g., 0*1 = 0, 0*0 = 0, 1*1 = 1) .
OR operations
Bitwise Inclusive OR : |
If either bit of the two corresponding bits is 1 then return 1.
XOR operation
Bitwise Exclusive XOR : ^
If both bits are the same, return 0. If the bits are different, return 1.
NOT operation
Bitwise NOT / complement : ~
Performs a bitwise inversion which means 1001 becomes 0110.
Example:
def not_a():
a = 5 # 0101
return ~a # returns -6 (1010)
The bitwise complement character (~) reverses each bit and returns the twos' complement number, so ~x is equivalent to -(x+1).
Important
Notice that if you print a negative number in binary in Python you won't see the flipped/reversed value (e.g., ~1001=0110), this is because Python does not print the actual binary bits but instead converts the number to a binary string that returns the signed magnitude method (e.g., ~1001=-1001).
A brief overview of twos' complement
The important thing to know is that the bitwise complement character reverses each bit (e.g., 1 becomes 0 or 0 becomes 1). However, if you expected ~5 to be -5, or are curious about how twos' complement works, it may be of interest that behind-the-scenes, Python (and most other languages) implements twos' complement representation*.
*It's important to note that twos' complement is just a storage implementation detail, you'll almost never need to think about this when doing bitwise equations as it doesn't represent the underlying binary values themselves.
Twos' complement wheel (4-bit numbers)
In the wheel diagram below, notice that positive numbers are in the expected binary format (e.g., 310 is 00112) that match our outer unsigned representation. However, notice the negative numbers use the remaining bit placements to count down from -8, for example instead of 810 as 10002 we have -810 as 10002, instead of 910 as 10012 we have -710, and so on.
Notice in the center of the wheel we're representing the bitwise complement of 5, so when you look at the twos' complement (where all the bits are flipped) of 5 we get an integer value of -6:
Binary Left and Right Shifting
Shift right : >>
Shift left : <<
Bit shifting simply moves the bits to the left or right by n places. When left shifting we push all bits by n towards the left. When right shifting we push all bits by n towards the right. Bit shifting makes multiplying or dividing by factors of 2 extremely easy.
Right shift 4-bit number
Shifting right slides our bits over by n to the right. So 1,1,0,1 (13) after shifting right by 2 becomes 0,0,1,1 (3).
Left shift 4-bit number
Shifting left slides our bits over by n to the left. Our original bit array was 0,0,1,1 (3). After left shifting by 2 we have 1,1,0,0 (12).
Bitmasking
Masking is when we flip one set of bits on or off based on another set of bits (called a mask or bitmask).
Check if a number is odd with a simple bitmask
You might normally use something like n % 2 == 0 to check if an integer is even or odd, however, using a bitmask is typically more performant and quite simple:
n = 6
is_odd = (n & 1) != 0
With 1 being the mask. In this instance we are using the mask to get the least significant bit, for example, 01102 (610) & 00012 (110) would return 0 and since 0 is equal to 0, we return False (6 is not odd). If we look at 0101 (510) & 0001 (110) we would get 1 so we return True since 1 is not equal to 0 (5 is odd).
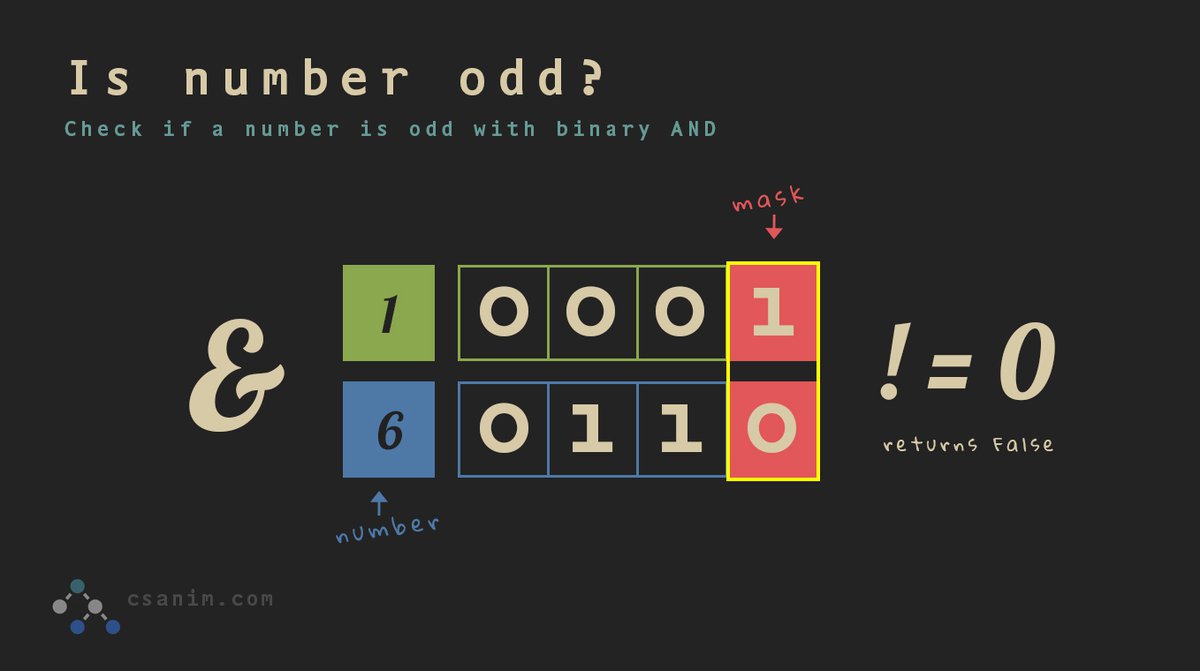
We will see several more examples of masks used below in common bit functions.
Common bit functions
Get bit
Get bit at i position:
def get_bit(n: int, i: int) -> int:
return (n & (1 << i)) != 0

Set bit
Makes sure bit at i'th place is set to 1:
def set_bit(n: int, i: int) -> int:
return n | (1 << i)
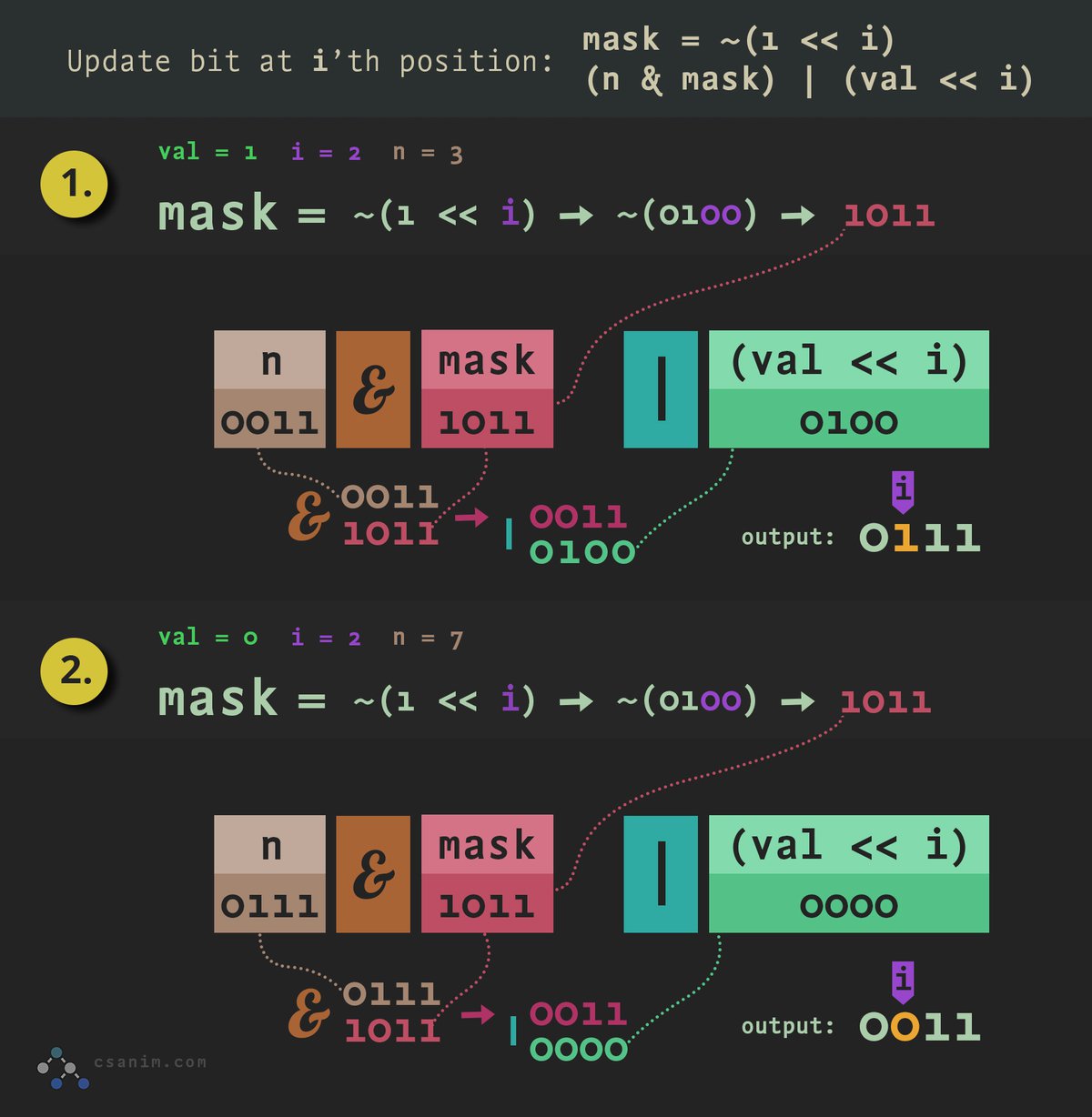
Update bit
Update bit at i position to a new value:
def update_bit(n: int, val: int, i: int) -> int:
mask = ~(1 << i)
return (n & mask) | (val << i)
The mask sets all bits to 1 except the i'th bit is 0.
We first use the mask to set bit at i'th position to 0 (n & mask) we then flip the i'th bit to 1 if val is 1.
In the graphic below we'll look at flipping a bit on (1.) and off (2.):
Clear bit
Set bit at i'th position to 0:
def clear_bit(n: int, i: int) -> int:
mask = ~(1 << i)
return n & mask

Reverse Bits
Let's look out how we might reverse the bits in any given unsigned integer.
Addition with binary numbers
You can add two integers together (e.g., 2 + 3) with bit operations as shown in the animation below:
Let's break this down with some simple examples:
*Note: We use 4-bit numbers in all examples below
Let's sum 1 + 1 in binary:
If we sum 0001 + 0001 the final result would be 2 or 0010, as you can see, the overlapping ones bits are carried up 1 place to return 0010.
Let's look at summing 1 + 2 in binary:
In binary 1 + 2 looks like 0001 + 0010, we don't need to carry any ones bits as they don't overlap, so we can just merge the ones bits to return 0011 (310).
Now, let's look at larger numbers:
Where it gets a little bit more complicated is when we need to sum slightly larger binary numbers that may have overlapping bits that need to be carried over several iterations.
Let's sum 2 + 3 in binary:
(1). So 0010 + 0011 requires us to first, find and carry the overlapping bits, in this case 0010 & 0011 would return 0010 as the bits that need to be carried. After carrying up 1 place (e.g., left shifting 1) we get b = 0100.
(2). Next, we find the uncarried bits at variable a, to do this we can XOR the tmp value (b before our AND operation) with a to get 0010 ^ 0011 = 0001.
(3). At this point, the carried bits b are 0100 and the uncarried bits a are 0001.
(4). We loop through again this time with our tmp value changing to 0100 and once again check if any more bits need carrying with our AND operation, however, this time we get 0010 & 0001 so b will now equal 0000.
(5). We then run the final XOR check at variable a = 0100 ^ 0001 which returns our sum of 0101 or 5.
See the interactive graphic below for a simple visualization of the above process (hover the highlighted numbers for tooltips):

Binary real numbers
Previously we only looked at integer numbers, typically any binary manipulation you do in day-to-day modern programming languages will be with integers. However, the way computers handle numbers with a fractional part is fairly interesting and can have some real-world ramifications.
In the following sections, we'll briefly cover two ways of representing real numbers (numbers with a fractional part) in binary.
Fixed-point number representation
Fixed-point arithmetic is significantly faster than floating-point arithmetic, however, it doesn't offer the precision and range of floating-point representation and is therefore not as common as floating-point representation.
We know all digits to the left of the binary point carry a weight of 20, 21, 22, and so forth. Bits to the right simply reverse, so they carry weights of 2-1, 2-2, 2-3, and so on:
Review the graphics below for example numbers represented in fixed-point binary:
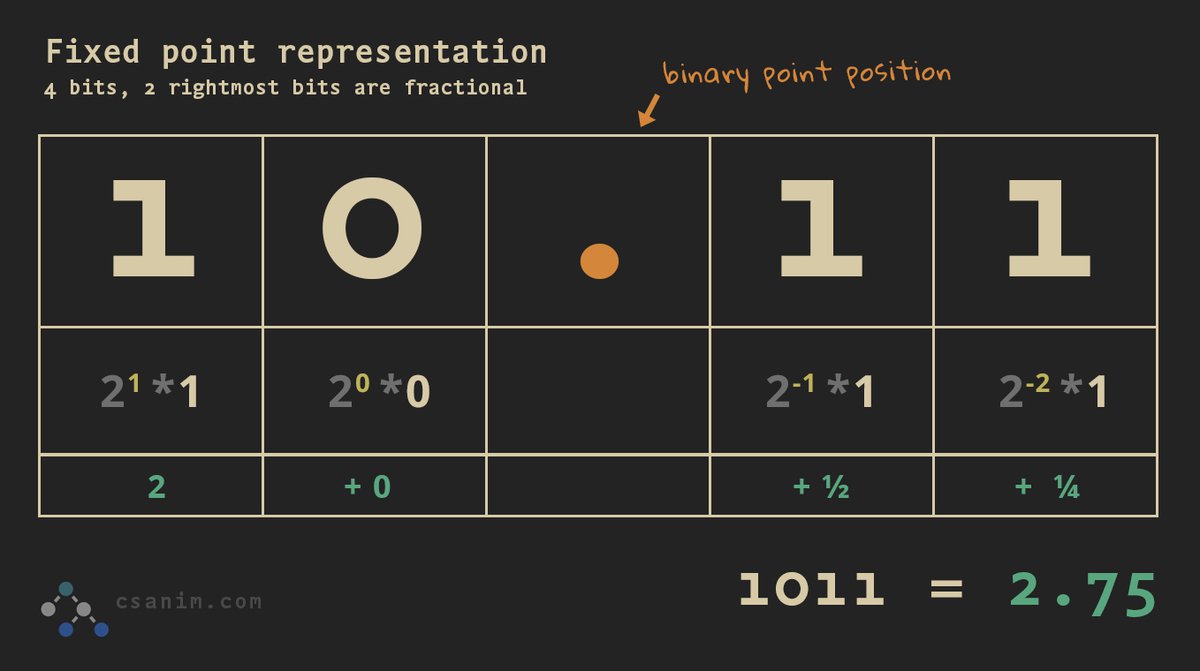
Binary 4-bit fixed point number
Each bit place is raised by decreasing powers of 2, so we get (2-1 = .5) + (2-2 = .25) = .75
Floating-point binary number representation
Using floating-point arithmetic, computers can display a large variety of numbers using a sliding window of precision (i.e., larger numbers are less precise: [100000.0]01, smaller numbers are more precise: [0.000001]). This is because we can design an algorithm that allows a set amount of available bits (commonly 32 or 64 bits) and uses these available bits to represent floating-point numbers.
Essentially we can have a single binary number array that tells us if a number is positive or negative, has a very high level of precision appropriate to the scale of the number, and gives us both the fractional and non-fractional parts.
The IEEE 754 floating-point format is how nearly all modern CPUs represent non-integer numbers.
The IEEE floating-point method was standardized in 1985 and has now been adopted by nearly all CPU manufacturers, before the IEEE standard, each microprocessor manufacturer designed their own proprietary floating-point representation method, thereby forcing expensive software rewrites just to target multiple computer brands or models.
The IEEE Standard 754 - 1985 for Binary Floating-Point Arithmetic took nearly a decade to solidify by 92 mathematicians, computer scientists and engineers, computer manufacturers, and microporocessor companies
The two most common IEEE standard floating-point binary storage formats are:
- IEEE Short Real (32-bits) / single precision: 1 bit for the sign, 8 bits exponent, 23 bits mantissa
- IEEE Long Real (64-bits) / double precision: 1 bit for the sign, 11 bits exponent, 52 bits mantissa
As the two are identical other than bit length, we'll focus on the single-precision (32-bits) format for simplicity:
Convert from decimal number to IEEE standard floating-point representation:
Let's convert 5.25 in the following example:
- Convert to fixed-point binary: 101.01
- Normalize by right shifting 2 until the binary point is behind the first 1s digit, normalized number is 1.0101, exponent is 2
- Add a bias of 127 to the exponenta1: 127 + 2 = 129
- Convert biased exponent (129) to 8-bit binary: 10000001
- Get the mantissa which are the numbers on the right side of the point after normalizing: 0101 (the leading 1 is implicit so we don't need to store it)
- Add the leading sign bit (positive is 0, negative is 1): 0
- All together: 0 10000001 01010000000000000000000
a1A bias is used so that we can represent both negative and positive exponents as an unsigned 8-bit binary number
Convert IEEE floating-point to decimal number:
Let's convert 0 10000001 01010000000000000000000 in the following example:
- Get the leading sign bit: 0 - this is a positive number
- Get the exponent bits: 10000001
- Convert exponent bits to base-10 integer: 129
- Subtract bias from exponent: 129 - 127 = 2
- Raise 2 to the power of our exponent from step 4 (which is also 2 in this case): 22 = 4
- Get the mantissa bits:01010000000000000000000
- We can ignore all the trailing zeros and focus on the first part: 0101
- Convert the mantissa to decimalb1: 0101 = 0 * (2-1) + 1 * (2-2) + 0 * (2-3) + 1 * (2-4) = 0 + .25 + 0 + 0.0625 = .3125
- Use the implicit bit convention rule to add 1 to our mantissa: 1 + .3125 = 1.3125
- Multiply exponent from step 5 with the mantissa from step 9: 4 * 1.3125 = 5.25
b1Each bit place in the mantissa is made up of 2 raised to decreasing powers of 2: 2-1,2-2,2-3,2-4
Convert float to binary string with python
Let's look at a simple method of converting a floating-point number to binary in Python.
Note: This is a question you might see asked in a technical interview to gauge one's familiarity with binary numbers, we are using a high-level language (Python) to concatenate strings to represent a binary number - we aren't manipulating real binary numbers.
Can you convert floats > 1?
Notice in our code we are returning Error for any number >= 1. Once you fully understand the code below, try making modifications to convert any positive number to binary (e.g., 1.8, 1, .5).
Converting a float number to a binary string is fairly straightforward.
Let's look at converting .75 to it's binary equivalent below
First we call our float_to_binary function:
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
Next, we simply check that this is a valid float number less than 1.
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
We initialize our binary string variable (binary_str) and our bit place variable (place), our binary string var will return the binary representation of our decimal number n with a radix point as the first character.
The place variable will be used to check the value of each bit place, we initialize at .5 since .5 is the highest value that our decimal bits can represent (remember: binary .1 is equal to decimal .5, binary .01 is equal to decimal .25, and so on).
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
Loop through until all numbers in our float n have been converted to bits.
We are limiting to 32 bits of precision, so if the binary number is longer than 32 bits we just return the current value:
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
In each loop iteration, we check if the current n value is >= to the current place value, and if so then we know that we need to add 1 to our bit string.
Our initial floating-point value n is .75, which is greater than place (.5), so we know we need to add '1' to our binary string and subtract place (.5) from n (.75), therefore the new value of n is now .25.
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
Next, we divide place in half, this means .5 becomes .25 in the second loop, which becomes .125 in the third loop, and so on:
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
This wraps up our main loop, we simply continue repeating the above process until our binary string limit is exceeded or n is equal to 0.
Once all calculations are done in our loop (and if our number doesn't exceed our 32-bit limit) we go ahead and return our binary string:
float_to_binary
def float_to_binary(n: float) -> str:
if n >= 1 or n <= 0:
return 'Error'
binary_str = '.'
place = 0.5
while n > 0:
if len(binary_str) >= 32:
# limit to 32 bits of precision
return binary_str
if n >= place:
binary_str += '1'
n -= place
else:
binary_str += "0"
place /= 2.0
return binary_str
float_to_binary(.75)
This wraps up our intro to bits article
This is a fairly long article, so congratulations on making it through the whole thing! For most purposes you should now have a good understanding of bitwise operations and how the binary number system works.



